Abele (village), Abele Ambrosini, Abele Blanc

Abele (Dorf): Abele ist ein kleines Dorf oder ein Weiler in der Stadt Poperinge in der belgischen Provinz Westflandern. Das Dorf liegt auf dem Territorium von Poperinge und seiner "deelgemeente" Watou, aber auch teilweise auf französischem Territorium. Abele hat ungefähr 600 Einwohner, von denen ungefähr 100 Franzosen sind. Die Hauptstraße fällt mit der Grenze zwischen Belgien und Frankreich zusammen, sodass sich Häuser auf verschiedenen Straßenseiten in einem anderen Land befinden.
Abele Ambrosini: Abele Ambrosini war eine italienische Partisanin.
Abele Blanc: Abele Blanc ist eine italienische Bergsteigerin. 2011 war er der zweiundzwanzigste, der die vierzehn Achttausender bestieg, nachdem er dies zwischen 1992 und 2011 getan hatte.
Argosy Foundation: Die 1997 gegründete Argosy Foundation hat ihren Sitz derzeit in Milwaukee, Wisconsin. Es war früher als Abele Family Charitable Trust bekannt.
Abele Nunatak: Abele Nunatak ist ein Nunatak, der 3 km östlich von Hutcheson Nunataks an der Spitze des Balchen-Gletschers im Marie-Byrd-Land liegt. Es wurde anhand von Vermessungen des United States Geological Survey (USGS) und der US Navy-Luftbilder von 1959 bis 1965 kartiert und später vom Beratenden Ausschuss für antarktische Namen (US-ACAN) nach CA Abele Jr., einem Mitglied von, benannt die Byrd Antarctic Expedition (1933–35).
Renzo Novatore: Abele Rizieri Ferrari, besser bekannt unter dem Pseudonym Renzo Novator, war ein italienischer Individualist Anarchist, Illegalismus und antifaschistischer Dichter, Philosophen und militant, jetzt vor allem für sein posthum veröffentlichtes Buch bekannt Gegen Creative - Nichts und im Zusammenhang mit ultra-modernistischen Tendenzen Futurismus. Sein Denken ist beeinflusst von Max Stirner, Friedrich Nietzsche, Georges Palante, Oscar Wilde, Henrik Ibsen, Arthur Schopenhauer und Charles Baudelaire.
Forrestal Range: Die Forrestal Range ist eine weitgehend schneebedeckte Bergkette mit einer Länge von etwa 105 km, die östlich des Dufek-Massivs und der Neptune Range im Pensacola-Gebirge der Antarktis liegt. Entdeckt und fotografiert am 13. Januar 1956 auf einem transkontinentalen Patrouillenflug der US Navy Operation Deep Freeze I vom McMurdo Sound in die Nähe des Weddellmeeres und zurück.
Abele spelen: Die abele spelen sind eine Sammlung von vier Stücken, die im Van Hulthem-Manuskript aus dem Jahr 1410 enthalten sind und sich in der Sammlung der Königlichen Bibliothek von Belgien in Brüssel befinden.
Ramón Abeledo: Ramón Gregorio Abeledo ist ein argentinischer Fußball-Mittelfeldspieler, der 1962 bei der FIFA-Weltmeisterschaft für Argentinien spielte. Er spielte auch für den Club Atlético Independiente.
Nacho Abeledo: Ignacio "Nacho" de Loyola Abeledo Rute ist ein spanischer Fußballspieler, der als linker Flügelspieler für CD San ​​Roque de Lepe spielt.
Ramón Abeledo: Ramón Gregorio Abeledo ist ein argentinischer Fußball-Mittelfeldspieler, der 1962 bei der FIFA-Weltmeisterschaft für Argentinien spielte. Er spielte auch für den Club Atlético Independiente.
Abeleh: Abeleh kann sich beziehen auf: Ableh (Begriffsklärung) Abeleh, Khuzestan
Abeleh, Khuzestan: Abeleh ist ein Dorf im Landkreis Rud Zard im Zentralbezirk des Landkreises Bagh-e Malek in der Provinz Khuzestan im Iran. Bei der Volkszählung 2006 wurde seine Existenz festgestellt, aber seine Bevölkerung wurde nicht gemeldet.
Ableh-ye Sofla: Ableh-ye Sofla ist ein Dorf im Landkreis Holayjan im Zentralbezirk des Landkreises Izeh in der Provinz Khuzestan im Iran. Bei der Volkszählung 2006 betrug die Einwohnerzahl 215 in 38 Familien.
Ableh-ye Sofla: Ableh-ye Sofla ist ein Dorf im Landkreis Holayjan im Zentralbezirk des Landkreises Izeh in der Provinz Khuzestan im Iran. Bei der Volkszählung 2006 betrug die Einwohnerzahl 215 in 38 Familien.
Manfred Abelein: Manfred Abelein war ein deutscher Politiker. Er war Vertreter der Deutschen Christlich-Demokratischen Union.
Abelemkpe: Abelenkpe ist ein Stadtgebiet im Stadtteil Accra, einem Stadtteil der Greater Accra Region in Ghana.
Abellen Sprache: Abellen , Abenlen , Aburlin oder Ayta Abellen ist eine sambalische Sprache. Es hat ungefähr 3.500 Sprecher und wird in einigen Aeta-Gemeinden in der Provinz Tarlac auf den Philippinen gesprochen. Ayta Abellen selbst gehört zur sambalischen Sprachfamilie auf den Philippinen und ist nicht nur eng mit den 5 anderen Ayta-Dialekten verwandt, sondern auch mit dem botolanischen Dialekt von Sambal.
Abellen Sprache: Abellen , Abenlen , Aburlin oder Ayta Abellen ist eine sambalische Sprache. Es hat ungefähr 3.500 Sprecher und wird in einigen Aeta-Gemeinden in der Provinz Tarlac auf den Philippinen gesprochen. Ayta Abellen selbst gehört zur sambalischen Sprachfamilie auf den Philippinen und ist nicht nur eng mit den 5 anderen Ayta-Dialekten verwandt, sondern auch mit dem botolanischen Dialekt von Sambal.
Abellen Sprache: Abellen , Abenlen , Aburlin oder Ayta Abellen ist eine sambalische Sprache. Es hat ungefähr 3.500 Sprecher und wird in einigen Aeta-Gemeinden in der Provinz Tarlac auf den Philippinen gesprochen. Ayta Abellen selbst gehört zur sambalischen Sprachfamilie auf den Philippinen und ist nicht nur eng mit den 5 anderen Ayta-Dialekten verwandt, sondern auch mit dem botolanischen Dialekt von Sambal.
Abellen Sprache: Abellen , Abenlen , Aburlin oder Ayta Abellen ist eine sambalische Sprache. Es hat ungefähr 3.500 Sprecher und wird in einigen Aeta-Gemeinden in der Provinz Tarlac auf den Philippinen gesprochen. Ayta Abellen selbst gehört zur sambalischen Sprachfamilie auf den Philippinen und ist nicht nur eng mit den 5 anderen Ayta-Dialekten verwandt, sondern auch mit dem botolanischen Dialekt von Sambal.
Leonardo Abelenda: Leonardo Daniel Abelenda Rodríguez ist ein uruguayischer Fußballspieler, der derzeit für die Plaza Colonia in der uruguayischen Segunda División spielt.
Leonardo Abelenda: Leonardo Daniel Abelenda Rodríguez ist ein uruguayischer Fußballspieler, der derzeit für die Plaza Colonia in der uruguayischen Segunda División spielt.
Abelemkpe: Abelenkpe ist ein Stadtgebiet im Stadtteil Accra, einem Stadtteil der Greater Accra Region in Ghana.
Jim Abeler: James J. Abeler II ist ein Politiker aus Minnesota und Mitglied des Senats von Minnesota. Als Mitglied der Republikanischen Partei von Minnesota vertritt er Distrikt 35 in der nördlichen Metropolregion Twin Cities. Zuvor vertrat er Distrikt 35A im Repräsentantenhaus von Minnesota.
Jim Abeler: James J. Abeler II ist ein Politiker aus Minnesota und Mitglied des Senats von Minnesota. Als Mitglied der Republikanischen Partei von Minnesota vertritt er Distrikt 35 in der nördlichen Metropolregion Twin Cities. Zuvor vertrat er Distrikt 35A im Repräsentantenhaus von Minnesota.
Abeles: Abeles ist ein englischer und jüdischer Familienname, abgeleitet vom biblischen Namen Abel. Bemerkenswerte Personen mit dem Nachnamen sind: Benjamin Abeles, amerikanischer Physiker Edward Abeles (1869–1919), amerikanischer Schauspieler Florin Abelès (1922–2005), französischer Physiker John H. Abeles, amerikanischer Geschäftsmann Kim Victoria Abeles, amerikanische Künstlerin Michele Abeles, amerikanischer Künstler Peter Abeles (1924–1999), australischer Geschäftsmann Moshe Abeles, israelischer Hirnforscher Norman Abeles, in Österreich geborener amerikanischer Psychologe Ruth Abeles, israelische olympische Turnerin Sigmund Abeles, amerikanischer figurativer Künstler
Benjamin Abeles: Benjamin Abeles war ein österreichisch-tschechischer Physiker, dessen Forschungen in den 1960er Jahren in den USA zu Germanium-Silizium-Legierungen zu der Technologie führten, mit der Raumsonden wie das Raumschiff Voyager angetrieben werden. Er wuchs in Österreich und der Tschechoslowakei auf und kam 1939 auf einer der Kindertransport- Missionen nach Großbritannien. Er schloss seine Ausbildung nach dem Krieg in der Tschechoslowakei und in Israel ab und promovierte in Physik. Anschließend lebte und arbeitete er als Forschungsphysiker in den USA und ging 1995 in den Ruhestand. Zu seinen Ehren zählen die Stuart Ballantine-Medaille von 1979 und seine Aufnahme in die New Jersey Inventors Hall of Fame (1991).
Peter Abeles: Sir Peter Emil Herbert Abeles , AC, war ein australischer Transportmagnat. Als Flüchtling aus Ungarn wurde er Geschäftsmann in Australien und 1972 zum Ritter geschlagen.
Transfer-Matrix-Methode (Optik): Die Übertragungsmatrixmethode ist eine Methode, die in der Optik und Akustik verwendet wird, um die Ausbreitung elektromagnetischer oder akustischer Wellen durch ein geschichtetes Medium zu analysieren. Dies ist beispielsweise relevant für die Gestaltung von Antireflexbeschichtungen und dielektrischen Spiegeln.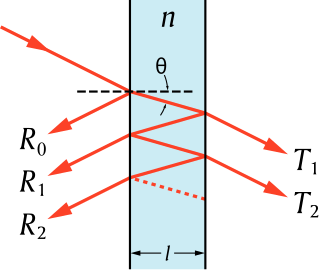
Abalessa: Abalessa ist eine Stadt und Gemeinde in der Provinz Tamanrasset im Süden Algeriens, die mit dem gleichnamigen Bezirk zusammenfällt. Laut der Volkszählung von 2008 hat es eine Bevölkerung von 9.163 gegenüber 6.484 im Jahr 1998, mit einer jährlichen Wachstumsrate von 3,6%. Abalessa liegt an der alten Trans-Sahara-Handelsroute, 80 Kilometer westlich der Stadt Tamanrasset, der Hauptstadt der Provinz. Die Postleitzahl der Stadt ist 11120.
Abalessa: Abalessa ist eine Stadt und Gemeinde in der Provinz Tamanrasset im Süden Algeriens, die mit dem gleichnamigen Bezirk zusammenfällt. Laut der Volkszählung von 2008 hat es eine Bevölkerung von 9.163 gegenüber 6.484 im Jahr 1998, mit einer jährlichen Wachstumsrate von 3,6%. Abalessa liegt an der alten Trans-Sahara-Handelsroute, 80 Kilometer westlich der Stadt Tamanrasset, der Hauptstadt der Provinz. Die Postleitzahl der Stadt ist 11120.
Johann Philipp Abelin: Johann Philipp Abelin war ein deutscher Chronist, dessen Karriere sich über das 16. und 17. Jahrhundert erstreckte. Er wurde wahrscheinlich in Straßburg geboren und starb dort zwischen 1634 und 1637. Er schrieb zahlreiche Geschichten unter den Pseudonymen Abeleus , Philipp Arlanibäus , Johann Ludwig Gottfried und Gotofredus .
Oxytrigona tataira: Oxytrigona tataira , allgemein bekannt als Tataíra oder Abelha-de-Fogo , ist eine Art von eusozialen stachellosen Bienen aus der Familie der Apidae und des Stammes Meliponini.
Abelhaleem Hasan Abdelraziq Ashqar: Abelhaleem Hasan Abdelraziq Ashqar ist ein palästinensischer muslimischer Aktivist, der kurzzeitig Assistenzprofessor für Wirtschaft an der Howard University war. Er wurde wegen Verachtung und Behinderung der Justiz verurteilt, weil er sich geweigert hatte, vor einer großen Jury in einem Prozess im Zusammenhang mit der Finanzierung der Hamas durch Spender in den USA auszusagen, und im November 2007 zu 135 Monaten Gefängnis verurteilt.
Abelhaleem Hasan Abdelraziq Ashqar: Abelhaleem Hasan Abdelraziq Ashqar ist ein palästinensischer muslimischer Aktivist, der kurzzeitig Assistenzprofessor für Wirtschaft an der Howard University war. Er wurde wegen Verachtung und Behinderung der Justiz verurteilt, weil er sich geweigert hatte, vor einer großen Jury in einem Prozess im Zusammenhang mit der Finanzierung der Hamas durch Spender in den USA auszusagen, und im November 2007 zu 135 Monaten Gefängnis verurteilt.
Abelheira: Abelheira ist ein Dorf in der portugiesischen Gemeinde Lourinhã.
Ābeļi Gemeinde: Die Gemeinde Ābeļi ist eine Verwaltungseinheit der Gemeinde Jēkabpils in Lettland.
Ābeļi Gemeinde: Die Gemeinde Ābeļi ist eine Verwaltungseinheit der Gemeinde Jēkabpils in Lettland.
Abelia: Abelia ist eine früher anerkannte Gattung, die etwa 30 Arten und Hybriden enthielt und zur Familie der Geißblätter Caprifoliaceae gehört. Molekulare phylogenetische Studien zeigten, dass die Gattung nicht monophyletisch war, und 2013 schlug Maarten Christenhusz die Fusion von Abelia mit Linnaea zusammen mit einigen anderen Gattungen vor. Abelia Abschnitt Zabelia wurde zur Gattung Zabelia erhoben .
Abelia (Organisation): Abelia ist ein Arbeitgeberverband in Norwegen, der unter der nationalen Konföderation norwegischer Unternehmen organisiert ist.
Abelia (Organisation): Abelia ist ein Arbeitgeberverband in Norwegen, der unter der nationalen Konföderation norwegischer Unternehmen organisiert ist.
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Abelia Kirche: Die Abelia-Dreifaltigkeitskirche ist eine georgisch-orthodoxe Kirche aus dem 13. Jahrhundert und befindet sich in der Gemeinde Tetri Tsqaro in der südzentralen Region von Georgien, Kvemo Kartli. Es ist ein einfaches Einschiff-Design und befindet sich am Rande des heutigen Dorfes Abeliani, das früher als Abelia bekannt war. Ein Hinweis auf die Diarchie in Georgien unter mongolischer Herrschaft in einer Inschrift an der Südwand der Kirche ermöglicht es, den Bau auf den Zeitraum von 1250 bis 1259 zu datieren. Die Kirche ist in die Liste der unbeweglichen Kulturdenkmäler von nationaler Bedeutung in Georgien eingetragen.
Zabelia corymbosa: Zabelia corymbosa ist eine Blütenpflanze aus der Familie der Geißblätter, Caprifoliaceae. Es stammt aus Zentralasien, wo es in Kasachstan, Kirgisistan und Tadschikistan vorkommt.
Linnaea spathulata: Linnaea spathulata , Synonym Abelia spathulata , ist eine Art von Linnaea aus der Familie der Geißblätter (Caprifoliaceae). Die Pflanze ist in Korea und Japan endemisch.
Linnaea floribunda: Linnaea floribunda ist eine in Mexiko beheimatete Blütenpflanze der Geißblattfamilie Caprifoliaceae. Es wird 4 m hoch und breit und ist ein halb immergrüner oder immergrüner Strauch mit glänzenden, eiförmigen Blättern und Büscheln von röhrenförmigen Cerise-Blüten mit einer Länge von bis zu 5 cm. Obwohl es bis zu –10 ° C winterhart ist, bevorzugt es einen geschützten Standort, zum Beispiel gegen eine nach Süden ausgerichtete Steinmauer.
Linnaea × Grandiflora: Linnaea × Grandiflora , Synonym Abelia × Grandiflora , ist eine Hybridart von Blütenpflanzen aus der Geißblattfamilie Caprifoliaceae, die durch Hybridisierung von L. chinensis mit L. uniflora gezüchtet wird .
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Linnaea floribunda: Linnaea floribunda ist eine in Mexiko beheimatete Blütenpflanze der Geißblattfamilie Caprifoliaceae. Es wird 4 m hoch und breit und ist ein halb immergrüner oder immergrüner Strauch mit glänzenden, eiförmigen Blättern und Büscheln von röhrenförmigen Cerise-Blüten mit einer Länge von bis zu 5 cm. Obwohl es bis zu –10 ° C winterhart ist, bevorzugt es einen geschützten Standort, zum Beispiel gegen eine nach Süden ausgerichtete Steinmauer.
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Linnaea spathulata: Linnaea spathulata , Synonym Abelia spathulata , ist eine Art von Linnaea aus der Familie der Geißblätter (Caprifoliaceae). Die Pflanze ist in Korea und Japan endemisch.
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Zabelia tyaihyonii: Zabelia tyaihyonii , Synonym Abelia mosanensis , bekannt als duftende Abelia , ist eine Laubstrauchart aus der Geißblattfamilie Caprifoliaceae. Mit einer Höhe von bis zu 2 Metern und einer Breite ist es härter als viele verwandte Arten und überlebt Temperaturen von bis zu -20 ° C (-4 ° F). Die röhrenförmigen Blüten sind rosa-weiß und stark duftend und erscheinen im späten Frühling. Die glänzend grünen Blätter färben sich im Herbst rot, bevor sie fallen.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Linnaea chinensis: Linnaea chinensis , Synonyme Abelia chinensis und Abelia rupestris , ist eine blühende Pflanzenart aus der Geißblattfamilie Caprifoliaceae. Es wurde 1818 von Robert Brown beschrieben und 1872 in die Gattung Linnaea überführt , obwohl dieser Schritt erst 2013 allgemein akzeptiert wurde. Die Pflanze lebt in China, Taiwan und Japan. Es ist ein kompakter Laubstrauch mit rötlichen Stielen und glänzenden, kleinen Blättern, die vor dem Herbst rotbraun werden. Es ist eine der kältebeständigsten Arten innerhalb der Gattung.
Linnaea spathulata: Linnaea spathulata , Synonym Abelia spathulata , ist eine Art von Linnaea aus der Familie der Geißblätter (Caprifoliaceae). Die Pflanze ist in Korea und Japan endemisch.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Linnaea spathulata: Linnaea spathulata , Synonym Abelia spathulata , ist eine Art von Linnaea aus der Familie der Geißblätter (Caprifoliaceae). Die Pflanze ist in Korea und Japan endemisch.
Linnaea floribunda: Linnaea floribunda ist eine in Mexiko beheimatete Blütenpflanze der Geißblattfamilie Caprifoliaceae. Es wird 4 m hoch und breit und ist ein halb immergrüner oder immergrüner Strauch mit glänzenden, eiförmigen Blättern und Büscheln von röhrenförmigen Cerise-Blüten mit einer Länge von bis zu 5 cm. Obwohl es bis zu –10 ° C winterhart ist, bevorzugt es einen geschützten Standort, zum Beispiel gegen eine nach Süden ausgerichtete Steinmauer.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Zabelia tyaihyonii: Zabelia tyaihyonii , Synonym Abelia mosanensis , bekannt als duftende Abelia , ist eine Laubstrauchart aus der Geißblattfamilie Caprifoliaceae. Mit einer Höhe von bis zu 2 Metern und einer Breite ist es härter als viele verwandte Arten und überlebt Temperaturen von bis zu -20 ° C (-4 ° F). Die röhrenförmigen Blüten sind rosa-weiß und stark duftend und erscheinen im späten Frühling. Die glänzend grünen Blätter färben sich im Herbst rot, bevor sie fallen.
Linnaea parvifolia: Linnaea parvifolia , Synonym Abelia schumannii , ist eine Blütenpflanzenart aus der Familie der in Zentralchina heimischen Caprifoliaceae. Es ist ein halb immergrüner Strauch, der 2 m hoch und 3 m breit wird. Im Spätsommer und Herbst entstehen rosa Blüten mit roten Kelchen.
Linnaea × Grandiflora: Linnaea × Grandiflora , Synonym Abelia × Grandiflora , ist eine Hybridart von Blütenpflanzen aus der Geißblattfamilie Caprifoliaceae, die durch Hybridisierung von L. chinensis mit L. uniflora gezüchtet wird .
Linnaea × Grandiflora: Linnaea × Grandiflora , Synonym Abelia × Grandiflora , ist eine Hybridart von Blütenpflanzen aus der Geißblattfamilie Caprifoliaceae, die durch Hybridisierung von L. chinensis mit L. uniflora gezüchtet wird .
Linnaea × Grandiflora: Linnaea × Grandiflora , Synonym Abelia × Grandiflora , ist eine Hybridart von Blütenpflanzen aus der Geißblattfamilie Caprifoliaceae, die durch Hybridisierung von L. chinensis mit L. uniflora gezüchtet wird .
Abelian: Abelian kann sich beziehen auf:
Abelsche und tauberische Theoreme: In der Mathematik sind abelsche und tauberische Theoreme Theoreme, die Bedingungen für zwei Methoden zur Summierung divergierender Reihen ergeben, um dasselbe Ergebnis zu erzielen , benannt nach Niels Henrik Abel und Alfred Tauber. Die ursprünglichen Beispiele sind Abels Theorem, das zeigt, dass, wenn eine Reihe gegen eine Grenze konvergiert, ihre Abel-Summe dieselbe Grenze ist, und Taubers Theorem, das zeigt, dass wenn die Abel-Summe einer Reihe existiert und die Koeffizienten ausreichend klein sind, die Reihe gegen die Abel konvergiert Summe. Allgemeinere abelsche und tauberische Theoreme liefern ähnliche Ergebnisse für allgemeinere Summationsmethoden.
Abelian: Abelian kann sich beziehen auf:
Abelian: Abelian kann sich beziehen auf:
Abelsche 2-Gruppe: In der Mathematik ist eine abelsche 2-Gruppe ein höherdimensionales Analogon einer abelschen Gruppe im Sinne einer höheren Algebra, die ursprünglich von Alexander Grothendieck eingeführt wurde, als er abstrakte Strukturen um abelsche Sorten und Picard-Gruppen untersuchte. Genauer gesagt werden sie von Groupoiden gegeben die einen Bifunktor haben das wirkt formal wie die Hinzufügung einer abelschen Gruppe. Nämlich der Bifunktor hat einen Begriff von Kommutativität, Assoziativität und eine Identitätsstruktur. Obwohl dies eine ziemlich hohe und abstrakte Struktur zu sein scheint, gibt es mehrere Beispiele für abelsche 2-Gruppen. Einige von ihnen liefern Prototypen für komplexere Beispiele höherer algebraischer Strukturen wie abelsche n-Gruppen.
Abelsche Kategorie: In der Mathematik ist eine abelsche Kategorie eine Kategorie, in der Morphismen und Objekte hinzugefügt werden können und in der Kernel und Kokernel existieren und wünschenswerte Eigenschaften haben. Das motivierende prototypische Beispiel einer abelschen Kategorie ist die Kategorie der abelschen Gruppen Ab . Die Theorie entstand aus dem Bestreben, mehrere kohomologische Theorien von Alexander Grothendieck und unabhängig voneinander in der etwas früheren Arbeit von David Buchsbaum zu vereinen. Abelsche Kategorien sind sehr stabile Kategorien; Zum Beispiel sind sie regelmäßig und erfüllen das Schlangen-Lemma. Die Klasse der abelschen Kategorien wird unter mehreren kategorialen Konstruktionen geschlossen, beispielsweise ist die Kategorie der Kettenkomplexe einer abelschen Kategorie oder die Kategorie der Funktoren von einer kleinen Kategorie zu einer abelschen Kategorie ebenfalls abelisch. Diese Stabilitätseigenschaften machen sie in der homologischen Algebra und darüber hinaus unvermeidlich. Die Theorie hat Hauptanwendungen in der algebraischen Geometrie, Kohomologie und reinen Kategorietheorie. Abelsche Kategorien sind nach Niels Henrik Abel benannt.
Differential der ersten Art: In der Mathematik ist Differential der ersten Art ein traditioneller Begriff, der in den Theorien von Riemannschen Oberflächen und algebraischen Kurven für überall reguläre Differential-1-Formen verwendet wird. Bei einer komplexen Mannigfaltigkeit M ist ein Differential der ersten Art ω daher dasselbe wie eine 1-Form, die überall holomorph ist; bei einer nicht singulären algebraischen Sorte V wäre dies ein globaler Abschnitt der kohärenten Garbe Ω 1 der Kähler-Differentiale. In beiden Fällen hat die Definition ihren Ursprung in der Theorie der abelschen Integrale.
Abelsche Erweiterung: In der abstrakten Algebra ist eine abelsche Erweiterung eine Galois-Erweiterung, deren Galois-Gruppe abelisch ist. Wenn die Galois-Gruppe auch zyklisch ist, wird die Erweiterung auch als zyklische Erweiterung bezeichnet . In die andere Richtung wird eine Galois-Erweiterung als lösbar bezeichnet, wenn ihre Galois-Gruppe lösbar ist, dh wenn die Gruppe in eine Reihe normaler Erweiterungen einer abelschen Gruppe zerlegt werden kann.
Abelsche Sorte: In der Mathematik, insbesondere in der algebraischen Geometrie, der komplexen Analyse und der algebraischen Zahlentheorie, ist eine abelsche Varietät eine projektive algebraische Varietät, die auch eine algebraische Gruppe ist, dh ein Gruppengesetz hat, das durch reguläre Funktionen definiert werden kann. Abelsche Varietäten gehören gleichzeitig zu den am meisten untersuchten Objekten in der algebraischen Geometrie und sind unverzichtbare Werkzeuge für viele Forschungen zu anderen Themen in der algebraischen Geometrie und Zahlentheorie.
Abelsche Gruppe: In der Mathematik ist eine abelsche Gruppe , auch kommutative Gruppe genannt , eine Gruppe, in der das Ergebnis der Anwendung der Gruppenoperation auf zwei Gruppenelemente nicht von der Reihenfolge abhängt, in der sie geschrieben sind. Das heißt, die Gruppenoperation ist kommutativ. Mit Addition als Operation bilden die ganzen Zahlen und die reellen Zahlen abelsche Gruppen, und das Konzept einer abelschen Gruppe kann als Verallgemeinerung dieser Beispiele angesehen werden. Abelsche Gruppen sind nach dem Mathematiker Niels Henrik Abel aus dem frühen 19. Jahrhundert benannt.
Higgs-Mechanismus: Im Standardmodell der Teilchenphysik ist der Higgs-Mechanismus wesentlich, um den Erzeugungsmechanismus der Eigenschaft "Masse" für Eichbosonen zu erklären. Ohne den Higgs Mechanismus aller Bosonen (einer der beiden Klassen von Teilchen, die anderen Fermionen) würden massless betrachtet werden, aber Messungen zeigen , dass die W +, W - und Z 0 Bosonen haben tatsächlich relativ große Massen von etwa 80 GeV / c 2 . Das Higgs-Feld löst dieses Rätsel. Die einfachste Beschreibung des Mechanismus fügt dem Standardmodell ein Quantenfeld (das Higgs-Feld) hinzu, das den gesamten Raum durchdringt. Unterhalb einer extrem hohen Temperatur verursacht das Feld ein spontanes Brechen der Symmetrie während der Wechselwirkungen. Das Aufbrechen der Symmetrie löst den Higgs-Mechanismus aus und bewirkt, dass die Bosonen, mit denen es interagiert, Masse haben. Im Standardmodell bezieht sich der Ausdruck "Higgs-Mechanismus" speziell auf die Erzeugung von Massen für die schwachen W ± - und Z- Bosonen durch elektroschwache Symmetriebrechung. Der Large Hadron Collider am CERN gab am 14. März 2013 Ergebnisse bekannt, die mit dem Higgs-Teilchen übereinstimmen. Dies macht es äußerst wahrscheinlich, dass das Feld oder ein ähnliches Feld existiert, und erklärt, wie der Higgs-Mechanismus in der Natur abläuft.
Higgs-Mechanismus: Im Standardmodell der Teilchenphysik ist der Higgs-Mechanismus wesentlich, um den Erzeugungsmechanismus der Eigenschaft "Masse" für Eichbosonen zu erklären. Ohne den Higgs Mechanismus aller Bosonen (einer der beiden Klassen von Teilchen, die anderen Fermionen) würden massless betrachtet werden, aber Messungen zeigen , dass die W +, W - und Z 0 Bosonen haben tatsächlich relativ große Massen von etwa 80 GeV / c 2 . Das Higgs-Feld löst dieses Rätsel. Die einfachste Beschreibung des Mechanismus fügt dem Standardmodell ein Quantenfeld (das Higgs-Feld) hinzu, das den gesamten Raum durchdringt. Unterhalb einer extrem hohen Temperatur verursacht das Feld ein spontanes Brechen der Symmetrie während der Wechselwirkungen. Das Aufbrechen der Symmetrie löst den Higgs-Mechanismus aus und bewirkt, dass die Bosonen, mit denen es interagiert, Masse haben. Im Standardmodell bezieht sich der Ausdruck "Higgs-Mechanismus" speziell auf die Erzeugung von Massen für die schwachen W ± - und Z- Bosonen durch elektroschwache Symmetriebrechung. Der Large Hadron Collider am CERN gab am 14. März 2013 Ergebnisse bekannt, die mit dem Higgs-Teilchen übereinstimmen. Dies macht es äußerst wahrscheinlich, dass das Feld oder ein ähnliches Feld existiert, und erklärt, wie der Higgs-Mechanismus in der Natur abläuft.
Abelsches Integral: In der Mathematik ist ein abelsches Integral , benannt nach dem norwegischen Mathematiker Niels Henrik Abel, ein Integral in der komplexen Ebene der Form
Lügenalgebra: In der Mathematik ist eine Lie-Algebra ein Vektorraum zusammen mit einer Operation namens Lie-Klammer eine alternierende bilineare Karte , das befriedigt die jakobiische Identität. Der Vektorraum zusammen mit dieser Operation ist eine nicht assoziative Algebra, was bedeutet, dass die Lie-Klammer nicht unbedingt assoziativ ist.
Abelianische Lügengruppe: In der Geometrie ist eine abelsche Lie-Gruppe eine Lie-Gruppe, die eine abelsche Gruppe ist.
Abel-Polynome: Die Abel-Polynome in der Mathematik bilden eine Polynomsequenz, deren n- ter Term die Form hat
Abelsche und tauberische Theoreme: In der Mathematik sind abelsche und tauberische Theoreme Theoreme, die Bedingungen für zwei Methoden zur Summierung divergierender Reihen ergeben, um dasselbe Ergebnis zu erzielen , benannt nach Niels Henrik Abel und Alfred Tauber. Die ursprünglichen Beispiele sind Abels Theorem, das zeigt, dass, wenn eine Reihe gegen eine Grenze konvergiert, ihre Abel-Summe dieselbe Grenze ist, und Taubers Theorem, das zeigt, dass wenn die Abel-Summe einer Reihe existiert und die Koeffizienten ausreichend klein sind, die Reihe gegen die Abel konvergiert Summe. Allgemeinere abelsche und tauberische Theoreme liefern ähnliche Ergebnisse für allgemeinere Summationsmethoden.
Abelsche Sorte: In der Mathematik, insbesondere in der algebraischen Geometrie, der komplexen Analyse und der algebraischen Zahlentheorie, ist eine abelsche Varietät eine projektive algebraische Varietät, die auch eine algebraische Gruppe ist, dh ein Gruppengesetz hat, das durch reguläre Funktionen definiert werden kann. Abelsche Varietäten gehören gleichzeitig zu den am meisten untersuchten Objekten in der algebraischen Geometrie und sind unverzichtbare Werkzeuge für viele Forschungen zu anderen Themen in der algebraischen Geometrie und Zahlentheorie.
Assoziative Algebra: In der Mathematik ist eine assoziative Algebra eine algebraische Struktur mit kompatiblen Operationen der Addition, Multiplikation und einer skalaren Multiplikation mit Elementen in einem bestimmten Bereich. Die Additions- und Multiplikationsoperationen zusammen ergeben A die Struktur eines Rings; Die Additions- und Skalarmultiplikationsoperationen ergeben zusammen A die Struktur eines Vektorraums über K. In diesem Artikel verwenden wir auch den Begriff K- Algebra, um eine assoziative Algebra über dem Feld K zu bezeichnen . Ein erstes Standardbeispiel einer K- Algebra ist ein Ring quadratischer Matrizen über einem Feld K mit der üblichen Matrixmultiplikation.
Abelsche und tauberische Theoreme: In der Mathematik sind abelsche und tauberische Theoreme Theoreme, die Bedingungen für zwei Methoden zur Summierung divergierender Reihen ergeben, um dasselbe Ergebnis zu erzielen , benannt nach Niels Henrik Abel und Alfred Tauber. Die ursprünglichen Beispiele sind Abels Theorem, das zeigt, dass, wenn eine Reihe gegen eine Grenze konvergiert, ihre Abel-Summe dieselbe Grenze ist, und Taubers Theorem, das zeigt, dass wenn die Abel-Summe einer Reihe existiert und die Koeffizienten ausreichend klein sind, die Reihe gegen die Abel konvergiert Summe. Allgemeinere abelsche und tauberische Theoreme liefern ähnliche Ergebnisse für allgemeinere Summationsmethoden.
Abelsche und tauberische Theoreme: In der Mathematik sind abelsche und tauberische Theoreme Theoreme, die Bedingungen für zwei Methoden zur Summierung divergierender Reihen ergeben, um dasselbe Ergebnis zu erzielen , benannt nach Niels Henrik Abel und Alfred Tauber. Die ursprünglichen Beispiele sind Abels Theorem, das zeigt, dass, wenn eine Reihe gegen eine Grenze konvergiert, ihre Abel-Summe dieselbe Grenze ist, und Taubers Theorem, das zeigt, dass wenn die Abel-Summe einer Reihe existiert und die Koeffizienten ausreichend klein sind, die Reihe gegen die Abel konvergiert Summe. Allgemeinere abelsche und tauberische Theoreme liefern ähnliche Ergebnisse für allgemeinere Summationsmethoden.
Abelsche Kategorie: In der Mathematik ist eine abelsche Kategorie eine Kategorie, in der Morphismen und Objekte hinzugefügt werden können und in der Kernel und Kokernel existieren und wünschenswerte Eigenschaften haben. Das motivierende prototypische Beispiel einer abelschen Kategorie ist die Kategorie der abelschen Gruppen Ab . Die Theorie entstand aus dem Bestreben, mehrere kohomologische Theorien von Alexander Grothendieck und unabhängig voneinander in der etwas früheren Arbeit von David Buchsbaum zu vereinen. Abelsche Kategorien sind sehr stabile Kategorien; Zum Beispiel sind sie regelmäßig und erfüllen das Schlangen-Lemma. Die Klasse der abelschen Kategorien wird unter mehreren kategorialen Konstruktionen geschlossen, beispielsweise ist die Kategorie der Kettenkomplexe einer abelschen Kategorie oder die Kategorie der Funktoren von einer kleinen Kategorie zu einer abelschen Kategorie ebenfalls abelisch. Diese Stabilitätseigenschaften machen sie in der homologischen Algebra und darüber hinaus unvermeidlich. Die Theorie hat Hauptanwendungen in der algebraischen Geometrie, Kohomologie und reinen Kategorietheorie. Abelsche Kategorien sind nach Niels Henrik Abel benannt.
Abelsche Kategorie: In der Mathematik ist eine abelsche Kategorie eine Kategorie, in der Morphismen und Objekte hinzugefügt werden können und in der Kernel und Kokernel existieren und wünschenswerte Eigenschaften haben. Das motivierende prototypische Beispiel einer abelschen Kategorie ist die Kategorie der abelschen Gruppen Ab . Die Theorie entstand aus dem Bestreben, mehrere kohomologische Theorien von Alexander Grothendieck und unabhängig voneinander in der etwas früheren Arbeit von David Buchsbaum zu vereinen. Abelsche Kategorien sind sehr stabile Kategorien; Zum Beispiel sind sie regelmäßig und erfüllen das Schlangen-Lemma. Die Klasse der abelschen Kategorien wird unter mehreren kategorialen Konstruktionen geschlossen, beispielsweise ist die Kategorie der Kettenkomplexe einer abelschen Kategorie oder die Kategorie der Funktoren von einer kleinen Kategorie zu einer abelschen Kategorie ebenfalls abelisch. Diese Stabilitätseigenschaften machen sie in der homologischen Algebra und darüber hinaus unvermeidlich. Die Theorie hat Hauptanwendungen in der algebraischen Geometrie, Kohomologie und reinen Kategorietheorie. Abelsche Kategorien sind nach Niels Henrik Abel benannt.
Komplexitätsfunktion: In der Informatik ist die Komplexitätsfunktion einer Zeichenfolge, eine endliche oder unendliche Folge von Buchstaben aus einem Alphabet, die Funktion, die die Anzahl der unterschiedlichen Faktoren aus dieser Zeichenfolge zählt. Im Allgemeinen zählt die Komplexitätsfunktion einer Sprache, eine Menge endlicher Wörter über einem Alphabet, die Anzahl unterschiedlicher Wörter gegebener Länge.
Deckungsgruppe: In der Mathematik ist eine Abdeckungsgruppe einer topologischen Gruppe H ein Abdeckungsraum G von H, so dass G eine topologische Gruppe ist und die Abdeckungskarte p : G → H ein kontinuierlicher Gruppenhomomorphismus ist. Die Karte p wird als Deckungshomomorphismus bezeichnet . Ein häufig vorkommender Fall ist eine doppelte Abdeckungsgruppe , eine topologische Doppelabdeckung, in der H den Index 2 in G hat ; Beispiele hierfür sind die Spingruppen, Pin-Gruppen und Metaplektiker-Gruppen.
Differential der ersten Art: In der Mathematik ist Differential der ersten Art ein traditioneller Begriff, der in den Theorien von Riemannschen Oberflächen und algebraischen Kurven für überall reguläre Differential-1-Formen verwendet wird. Bei einer komplexen Mannigfaltigkeit M ist ein Differential der ersten Art ω daher dasselbe wie eine 1-Form, die überall holomorph ist; bei einer nicht singulären algebraischen Sorte V wäre dies ein globaler Abschnitt der kohärenten Garbe Ω 1 der Kähler-Differentiale. In beiden Fällen hat die Definition ihren Ursprung in der Theorie der abelschen Integrale.
Abelsche Erweiterung: In der abstrakten Algebra ist eine abelsche Erweiterung eine Galois-Erweiterung, deren Galois-Gruppe abelisch ist. Wenn die Galois-Gruppe auch zyklisch ist, wird die Erweiterung auch als zyklische Erweiterung bezeichnet . In die andere Richtung wird eine Galois-Erweiterung als lösbar bezeichnet, wenn ihre Galois-Gruppe lösbar ist, dh wenn die Gruppe in eine Reihe normaler Erweiterungen einer abelschen Gruppe zerlegt werden kann.
Abelsche Erweiterung: In der abstrakten Algebra ist eine abelsche Erweiterung eine Galois-Erweiterung, deren Galois-Gruppe abelisch ist. Wenn die Galois-Gruppe auch zyklisch ist, wird die Erweiterung auch als zyklische Erweiterung bezeichnet . In die andere Richtung wird eine Galois-Erweiterung als lösbar bezeichnet, wenn ihre Galois-Gruppe lösbar ist, dh wenn die Gruppe in eine Reihe normaler Erweiterungen einer abelschen Gruppe zerlegt werden kann.
Abelsche Sorte: In der Mathematik, insbesondere in der algebraischen Geometrie, der komplexen Analyse und der algebraischen Zahlentheorie, ist eine abelsche Varietät eine projektive algebraische Varietät, die auch eine algebraische Gruppe ist, dh ein Gruppengesetz hat, das durch reguläre Funktionen definiert werden kann. Abelsche Varietäten gehören gleichzeitig zu den am meisten untersuchten Objekten in der algebraischen Geometrie und sind unverzichtbare Werkzeuge für viele Forschungen zu anderen Themen in der algebraischen Geometrie und Zahlentheorie.
Messgerätetheorie: In der Physik ist eine Eichentheorie eine Art Feldtheorie, bei der sich der Lagrange unter lokalen Transformationen bestimmter Lie-Gruppen nicht ändert.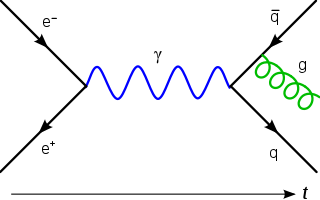
Mathematischer Witz: Ein mathematischer Witz ist eine Form von Humor, die sich auf Aspekte der Mathematik oder ein Stereotyp von Mathematikern stützt. Der Humor kann von einem Wortspiel oder von einer doppelten Bedeutung eines mathematischen Begriffs oder vom Missverständnis eines Laien über ein mathematisches Konzept herrühren. Der Mathematiker und Autor John Allen Paulos beschrieb in seinem Buch Mathematik und Humor verschiedene Arten, wie sich Mathematik, die allgemein als trockene, formale Aktivität angesehen wird, mit Humor überschneidet, einer lockeren, respektlosen Aktivität: Beide sind Formen des "intellektuellen Spiels"; beide haben "Logik, Muster, Regeln, Struktur"; und beide sind "wirtschaftlich und explizit".
Abelsche Gruppe: In der Mathematik ist eine abelsche Gruppe , auch kommutative Gruppe genannt , eine Gruppe, in der das Ergebnis der Anwendung der Gruppenoperation auf zwei Gruppenelemente nicht von der Reihenfolge abhängt, in der sie geschrieben sind. Das heißt, die Gruppenoperation ist kommutativ. Mit Addition als Operation bilden die ganzen Zahlen und die reellen Zahlen abelsche Gruppen, und das Konzept einer abelschen Gruppe kann als Verallgemeinerung dieser Beispiele angesehen werden. Abelsche Gruppen sind nach dem Mathematiker Niels Henrik Abel aus dem frühen 19. Jahrhundert benannt.
Abelsche Gruppe: In der Mathematik ist eine abelsche Gruppe , auch kommutative Gruppe genannt , eine Gruppe, in der das Ergebnis der Anwendung der Gruppenoperation auf zwei Gruppenelemente nicht von der Reihenfolge abhängt, in der sie geschrieben sind. Das heißt, die Gruppenoperation ist kommutativ. Mit Addition als Operation bilden die ganzen Zahlen und die reellen Zahlen abelsche Gruppen, und das Konzept einer abelschen Gruppe kann als Verallgemeinerung dieser Beispiele angesehen werden. Abelsche Gruppen sind nach dem Mathematiker Niels Henrik Abel aus dem frühen 19. Jahrhundert benannt.
Abelsches Integral: In der Mathematik ist ein abelsches Integral , benannt nach dem norwegischen Mathematiker Niels Henrik Abel, ein Integral in der komplexen Ebene der Form
Lokalisierungsformel für die äquivariante Kohomologie: In der Differentialgeometrie heißt es in der Lokalisierungsformel : für eine äquivariant geschlossene äquivariante Differentialform auf einem Orbifold M mit einer Toruswirkung und für eine ausreichend kleine in der Lie-Algebra des Torus T ,
Abweichende Serien: In der Mathematik ist eine divergente Reihe eine unendliche Reihe, die nicht konvergent ist, was bedeutet, dass die unendliche Folge der Teilsummen der Reihe keine endliche Grenze hat.
Monoid: In der abstrakten Algebra, einem Zweig der Mathematik, ist ein Monoid eine Menge, die mit einer assoziativen binären Operation und einem Identitätselement ausgestattet ist.
Klassenfeldtheorie: In der Mathematik ist die Klassenfeldtheorie der Zweig der algebraischen Zahlentheorie, der sich mit den abelschen Erweiterungen von Zahlenfeldern, globalen Feldern mit positiven Eigenschaften und lokalen Feldern befasst. Die Theorie hatte ihren Ursprung im Beweis der quadratischen Reziprozität durch Gauß Ende des 18. Jahrhunderts. Diese Ideen wurden im Laufe des nächsten Jahrhunderts entwickelt und führten zu einer Reihe von Vermutungen von Hilbert, die später von Takagi und Artin bewiesen wurden. Diese Vermutungen und ihre Beweise bilden den Hauptteil der Klassenfeldtheorie.
Idempotent (Ringtheorie): In der Ringtheorie ist ein idempotentes Element oder einfach ein idempotentes Element eines Rings ein Element a, so dass a 2 = a . Das heißt, das Element ist unter der Multiplikation des Rings idempotent. Induktiv kann man dann auch schließen, dass a = a 2 = a 3 = a 4 = ... = a n für jede positive ganze Zahl n ist . Beispielsweise ist ein idempotentes Element eines Matrixrings genau eine idempotente Matrix.
Abelsches Sandhaufenmodell: Das abelsche Sandhaufenmodell , auch als Bak-Tang-Wiesenfeld-Modell bekannt , war das erste entdeckte Beispiel für ein dynamisches System mit selbstorganisierter Kritikalität. Es wurde 1987 von Per Bak, Chao Tang und Kurt Wiesenfeld in einem Artikel vorgestellt.
Abelsches Sandhaufenmodell: Das abelsche Sandhaufenmodell , auch als Bak-Tang-Wiesenfeld-Modell bekannt , war das erste entdeckte Beispiel für ein dynamisches System mit selbstorganisierter Kritikalität. Es wurde 1987 von Per Bak, Chao Tang und Kurt Wiesenfeld in einem Artikel vorgestellt.
Abelsche Sorte: In der Mathematik, insbesondere in der algebraischen Geometrie, der komplexen Analyse und der algebraischen Zahlentheorie, ist eine abelsche Varietät eine projektive algebraische Varietät, die auch eine algebraische Gruppe ist, dh ein Gruppengesetz hat, das durch reguläre Funktionen definiert werden kann. Abelsche Varietäten gehören gleichzeitig zu den am meisten untersuchten Objekten in der algebraischen Geometrie und sind unverzichtbare Werkzeuge für viele Forschungen zu anderen Themen in der algebraischen Geometrie und Zahlentheorie.
Halbgruppe: In der Mathematik ist eine Halbgruppe eine algebraische Struktur, die aus einer Menge zusammen mit einer assoziativen binären Operation besteht.
Garbe Module: In der Mathematik ist ein Bündel von O- Modulen oder einfach ein O- Modul über einem Ringraum ein Bündel F, so dass für jede offene Teilmenge U von X F ( U ) ein O ( U ) -Modul ist und die Restriktionskarten F ( U ) → F ( V ) sind kompatibel mit den Restriktionskarten O ( U ) → O ( V ): Die Restriktion von fs ist die Restriktion von f mal der von s für jedes f in O ( U ) und s in F. ( U ).
Abelsche Gruppe: In der Mathematik ist eine abelsche Gruppe , auch kommutative Gruppe genannt , eine Gruppe, in der das Ergebnis der Anwendung der Gruppenoperation auf zwei Gruppenelemente nicht von der Reihenfolge abhängt, in der sie geschrieben sind. Das heißt, die Gruppenoperation ist kommutativ. Mit Addition als Operation bilden die ganzen Zahlen und die reellen Zahlen abelsche Gruppen, und das Konzept einer abelschen Gruppe kann als Verallgemeinerung dieser Beispiele angesehen werden. Abelsche Gruppen sind nach dem Mathematiker Niels Henrik Abel aus dem frühen 19. Jahrhundert benannt.
Abels Satz: In der Mathematik bezieht Abels Theorem für Potenzreihen eine Grenze einer Potenzreihe auf die Summe ihrer Koeffizienten. Es ist nach dem norwegischen Mathematiker Niels Henrik Abel benannt.
Abelsche Oberfläche: In der Mathematik ist eine abelsche Oberfläche eine zweidimensionale abelsche Sorte.
Abelsche und tauberische Theoreme: In der Mathematik sind abelsche und tauberische Theoreme Theoreme, die Bedingungen für zwei Methoden zur Summierung divergierender Reihen ergeben, um dasselbe Ergebnis zu erzielen , benannt nach Niels Henrik Abel und Alfred Tauber. Die ursprünglichen Beispiele sind Abels Theorem, das zeigt, dass, wenn eine Reihe gegen eine Grenze konvergiert, ihre Abel-Summe dieselbe Grenze ist, und Taubers Theorem, das zeigt, dass wenn die Abel-Summe einer Reihe existiert und die Koeffizienten ausreichend klein sind, die Reihe gegen die Abel konvergiert Summe. Allgemeinere abelsche und tauberische Theoreme liefern ähnliche Ergebnisse für allgemeinere Summationsmethoden.
Abelsche Sorte: In der Mathematik, insbesondere in der algebraischen Geometrie, der komplexen Analyse und der algebraischen Zahlentheorie, ist eine abelsche Varietät eine projektive algebraische Varietät, die auch eine algebraische Gruppe ist, dh ein Gruppengesetz hat, das durch reguläre Funktionen definiert werden kann. Abelsche Varietäten gehören gleichzeitig zu den am meisten untersuchten Objekten in der algebraischen Geometrie und sind unverzichtbare Werkzeuge für viele Forschungen zu anderen Themen in der algebraischen Geometrie und Zahlentheorie.